what happens to kinetic energy weight in a stopped cars collide
It may not seem similar much, just driving even a few kilometres per hour in a higher place the speed limit greatly increases the take chances of an accident.
Many of united states cheat a little when driving. We figure that while the speed limit is 60 km/h the police won't pull united states over if we sit on 65. So we happily let the speedo hover just above the speed limit, unaware that past so doing we are greatly magnifying our chances of crashing.
Using information from bodily road crashes, scientists at the University of Adelaide estimated the relative gamble of a car becoming involved in a casualty crash—a auto crash in which people are killed or hospitalised—for cars travelling at or above 60 km/h. They found that the adventure approximately doubled for every 5 km/h higher up sixty km/h. Thus, a car travelling at 65 km/h was twice as likely to be involved in a casualty crash as one travelling at lx km/h. For a car travelling at 70 km/h the risk increased fourfold. For speeds below 60 km/h the likelihood of a fatal crash can be expected to exist correspondingly reduced.
Stopping distance calculator
Small conditions can make a large divergence to the time information technology takes yous to stop your car, such as going a few km/hr slower or existence alert on the road.
Interactive
? km/h
? sec
? m/s2
metres
travelled before car stops
metres
travelled earlier brakes are fully applied
metres travelled before auto stops
metres travelled before brakes are fully applied

The physics that drive y'all
Reaction time
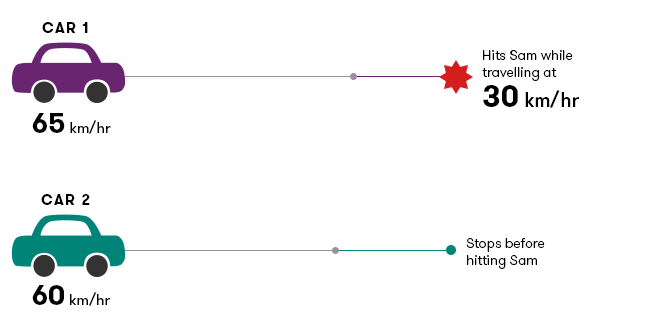
I reason for this increased take chances is reaction fourth dimension—the fourth dimension it takes between a person perceiving a danger and reacting to it. Consider this example. Ii cars of equal weight and braking power are travelling along the same road. Car 1, travelling at 65 km/h, is overtaking Car 2, which is travelling at sixty km/h. A child on a bicycle—let's call him Sam—emerges from a driveway simply as the two cars are side-by-side. The drivers both see the child at the same time and both take 1.5 seconds before they fully employ the brakes. In those few moments, Car 1 travels 27.ane metres and Car two travels 25.0 metres.

The divergence of two.1 metres might seem relatively small, but combined with other factors it could mean the divergence between life and death for Sam.
The figure of i.v seconds is the reaction time of average drivers. A driver who is distracted, for instance listening to loud music, using a mobile phone or has drunkard booze may take as long every bit three seconds to react.
Braking altitude
The braking altitude (the altitude a car travels before stopping when the brakes are applied) depends on a number of variables. The gradient or grade of the roadway is of import—a car will stop more quickly if it is going uphill because gravity will help. The frictional resistance between the road and the automobile's tyres is also important—a machine with new tyres on a dry out road will be less likely to skid and volition stop more rapidly than one with worn tyres on a wet road. If slope and frictional resistance are equal, the cistron that has nigh influence on braking distance is initial speed.
The formula used to calculate braking distance can be derived from a general equation of physics:
$$V_{f}^{ii} = V_{0}^{ii} - 2ad$$
where Vf is the terminal velocity, V0 is the initial velocity, a is the rate of deceleration and d is the distance travelled during deceleration. Since we know that Fivef will be zero when the car has stopped, this equation tin be re-written as:
$$d = V_{0}^{2} / 2a$$
From this we can see that braking altitude is proportional to the square of the speed—which means that it increases considerably as speed increases. If we assume that a is 10 metres per second per second and assume that the route is apartment and the braking systems of the two cars are equally effective, we can now calculate braking distance for cars 1 and two in our example. For car 1, d = sixteen.3 metres, while for Motorcar 2, d = xiii.9 metres.
Adding reaction altitude to braking distance, the stopping distance for Car i is 27.1 + 16.3 = 43.4 metres. For Automobile two, stopping distance is 25 + 13.nine = 38.ix metres. Car 1 therefore takes four.5 more metres to stop than Automobile 2, a 12 per cent increase.

Nosotros tin now see why Car one is more likely than Machine ii to hit Sam. If Sam is forty metres from the cars when the drivers run across him, Machine 2 will stop just in time. Automobile one, though, will turn straight into him. By re-writing the start equation, we can calculate the speed at which the collision occurs:
$$V_{f} = \sqrt{V_{0}^{2} - 2ad} = 8.2\mbox{ }metres\mbox{ }per\mbox{ }2d$$
(where d = 40 metres minus the reaction distance of 27.1 metres = 12.ix metres).
Thus, the impact occurs at near thirty kilometres/60 minutes, probably fast plenty to kill Sam. If the car's initial speed was 70 kilometres/hour, the impact velocity would be 45 kilometres/hour, more than fast enough to impale.
These calculations assume that the driver has an average reaction time. If the commuter is distracted and has a longer than average reaction fourth dimension, then he or she may hit Sam without having applied the brakes at all.
Touch on a pedestrian
Because the pedestrian, Sam, is and so much lighter than the machine, he has piffling event upon its speed. The auto, even so, very apace increases Sam'southward speed from aught to the bear on speed of the vehicle. The fourth dimension taken for this is about the fourth dimension it takes for the car to travel a altitude equal to Sam's thickness—most 20 centimetres. The impact speed of Automobile 1 in our example is about 8.2 metres per second, and so the affect lasts only about 0.024 seconds. Sam must be accelerated at a rate of about 320 metres per second per second during this short time. If Sam weighs 50 kilograms, and then the force required is the production of his mass and his dispatch—about xvi,000 newtons or nigh one.6 tonnes weight.
Since the impact force on Sam depends on the impact speed divided by the impact time, it increases as the square of the impact speed. The impact speed, every bit nosotros take seen above, increases rapidly every bit the travel speed increases, because the brakes are unable to bring the machine to a stop in time.
Once a pedestrian has been hit by a car, the probability of serious injury or death depends strongly on the bear upon speed. Reducing the bear upon speed from 60 to 50 kilometres/hour well-nigh halves the likelihood of death, merely has relatively trivial influence on the likelihood of injury, which remains close to 100 per cent. Reducing the speed to forty kilometres/hour, as in school zones, reduces the likelihood of death by a gene of 4 compared with 60 kilometres/hour, and of grade the likelihood of an bear on is likewise dramatically reduced.
Modern cars with depression streamlined bonnets are more than pedestrian-friendly than upright designs, such as those found in 4-wheel drive vehicles, since the pedestrian is thrown upwards towards the windscreen with a corresponding slowing of the affect. Cars with bull-bars are particularly unfriendly to pedestrians and to other vehicles, since they are designed to protect their own occupants with footling regard for others.
Impact on a large object
If, instead of hitting a pedestrian, the automobile hits a tree, a brick wall, or another heavy object, so the car'south energy of motion (kinetic energy) is all dissipated when the automobile body is bent and smashed. Since the kinetic energy (E) is given past
$$E = (1/ii)\mbox{ }mass × speed^{ii}$$
it increases as the foursquare of the bear upon velocity. Driving a very heavy vehicle does not lessen the effect of the impact much because, although there is more metallic to absorb the bear on energy, at that place is as well more energy to exist absorbed.
Less control
At higher speeds cars become more hard to manoeuvre, a fact partly explained past Newton's First Law of Motion. This states that if the net forcefulness acting on an object is zero then the object will either remain at rest or proceed to motion in a straight line with no modify in speed. This resistance of an object to changing its state of rest or motion is called inertia . Information technology is inertia that will keep you moving when the car you are in comes to a sudden finish (unless y'all are restrained by a seatbelt).
To counteract inertia when navigating a bend in the road we need to use a strength—which nosotros do by turning the steering wheel to change the management of the tyres. This makes the car deviate from the direct line in which information technology is travelling and go round the bend. The force between the tyres and the route increases with increasing speed and with the sharpness of the turn (Strength = mass × velocity squared, divided past the radius of the turn), increasing the likelihood of an uncontrolled skid. High speed also increases the potential for driver mistake caused by over- or under-steering (turning the steering bicycle also far, thereby 'cutting the corner', or non far enough, so that the car hits the exterior shoulder of the road).
Killer speed
All these factors show that the chance of being involved in a prey crash increases dramatically with increasing speed. In the University of Adelaide written report referred to earlier, this was certainly true in zones where the speed limit was lx kilometres/hr: the hazard doubled with every five kilometres/hr higher up the speed limit. A corresponding decrease is to be expected in zones with lower speed limits.
You make up one's mind on your speed, but physics decides whether you live or die.TAC Road Safe Commercial
Conclusion
Is the risk worth it? In our hypothetical case, the driver of Automobile ii, travelling at the speed limit, would have had a nasty scare, but nothing more. The driver of Car 1, driving just 5 kilometres/hour above the limit, would not be so lucky: whether Sam had lived or died, the driver would face up legal proceedings, a possible jail sentence, and a whole lifetime of guilt.

chatfieldhappereand.blogspot.com
Source: https://www.science.org.au/curious/technology-future/physics-speeding-cars
0 Response to "what happens to kinetic energy weight in a stopped cars collide"
Post a Comment